Leonardo Fibonacci a mente !
Leonardo Pisano, mais conhecido como Fibonacci, foi um matemático italiano que viveu entre os séculos XII e XIII. É mais famoso pela sequência que leva seu nome, a Sequência de Fibonacci, mas suas contribuições para a matemática vão muito além disso. Este artigo explora a vida, as obras e o impacto de Fibonacci, destacando suas contribuições fundamentais para a matemática e as ciências.
Vida de Fibonacci
Contexto Histórico
Leonardo Fibonacci nasceu por volta de 1170 na cidade de Pisa, na Itália. Seu pai, Guglielmo Bonacci, era um comerciante próspero que trabalhou em um posto comercial em Bugia, na Argélia. Graças ao trabalho do pai, Fibonacci teve a oportunidade de viajar e estudar diferentes sistemas numéricos e métodos matemáticos ao redor do Mediterrâneo.
Educação e Viagens
Fibonacci recebeu uma educação em aritmética e álgebra durante suas viagens pelo Norte da África. Ele estudou métodos matemáticos em várias cidades mediterrâneas, como Bugia, Alexandria e Constantinopla. Esse contato com diferentes culturas e sistemas numéricos foi crucial para o desenvolvimento de suas ideias matemáticas.
Principais Obras

“Liber Abaci”
Descrição
- Título: “Liber Abaci” (O Livro do Ábaco)
- Publicado: 1202 (revisado em 1228)
- Conteúdo: Introdução ao sistema numérico hindu-arábico na Europa, que inclui o uso do zero, e métodos aritméticos e algébricos.
Impacto
- Sistema Numérico: O “Liber Abaci” apresentou à Europa o sistema decimal posicional e o uso do zero, que eram usados pelos matemáticos árabes e indianos. Esse sistema simplificou grandemente a aritmética e foi adotado gradualmente em toda a Europa.
- Problemas e Soluções: O livro inclui uma série de problemas práticos, como cálculo de lucros comerciais, conversão de moedas e sistemas de medidas, além da famosa Sequência de Fibonacci, introduzida através de um problema sobre o crescimento populacional de coelhos.
Sequência de Fibonacci
Definição
A Sequência de Fibonacci é uma série de números onde cada número é a soma dos dois anteriores, começando por 0 e 1. A sequência é definida como:
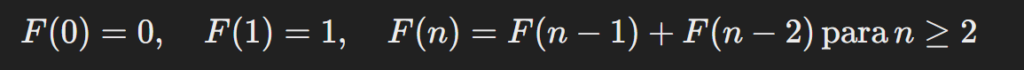
F(0)=0, F(1)=1, F(n)=F(n−1)+F(n−2) paran ≥2Exemplo de Termos
Os primeiros termos da Sequência de Fibonacci são:
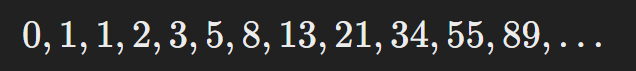
0,1,1,2,3,5,8,13,21,34,55,89,…Aplicações
- Matemática e Ciência: A sequência aparece em várias áreas, incluindo teoria dos números, computação e bioinformática.
- Natureza: A sequência e a proporção áurea, relacionada a ela, são encontradas em padrões naturais, como a disposição das folhas em uma planta, o arranjo das escamas em pinhas e a estrutura das conchas.
- Arte e Arquitetura: A proporção áurea é usada para criar composições equilibradas e esteticamente agradáveis.
“Practica Geometriae”
Descrição
- Título: “Practica Geometriae” (A Prática da Geometria)
- Publicado: 1220
- Conteúdo: Coleção de problemas e métodos geométricos, incluindo cálculos de áreas e volumes, e o uso de teoremas geométricos.
Impacto
- Aplicação Prática: O livro ofereceu técnicas práticas para agrimensores e engenheiros, fornecendo métodos precisos para medir terrenos e construir estruturas.
“Flos”
Descrição
- Título: “Flos” (A Flor)
- Publicado: 1225
- Conteúdo: Contém soluções para problemas matemáticos apresentados por Johannes of Palermo, incluindo equações cúbicas e quadráticas.
Impacto
- Desafios Matemáticos: Fibonacci demonstrou sua habilidade em resolver problemas complexos, consolidando sua reputação como um dos principais matemáticos de sua época.
“Liber Quadratorum”
Descrição
- Título: “Liber Quadratorum” (O Livro dos Quadrados)
- Publicado: 1225
- Conteúdo: Trata da teoria dos números, especialmente das propriedades dos números quadrados.
Impacto
- Teoria dos Números: Fibonacci explorou propriedades avançadas dos números, incluindo soluções para equações de segundo grau e relações entre números quadrados. Este trabalho é considerado um dos primeiros exemplos de investigação sistemática na teoria dos números.
“Di minor guisa”
Descrição
- Título: “Di minor guisa” (De forma menor)
- Conteúdo: Uma obra menor, provavelmente relacionada a métodos aritméticos práticos.
Impacto
- Aritmética Prática: Forneceu métodos adicionais para cálculos práticos, complementando as técnicas apresentadas no “Liber Abaci”.
Legado
Influência na Matemática
- Europa Medieval: As obras de Fibonacci introduziram conceitos matemáticos avançados que eram desconhecidos na Europa medieval, acelerando o desenvolvimento da matemática europeia.
- Sistemas Numéricos: A adoção do sistema numérico hindu-arábico facilitou cálculos e comércio, substituindo gradualmente o sistema romano.
Reconhecimento
- Nome Fibonacci: O nome Fibonacci, uma abreviação de “filius Bonacci” (filho de Bonacci), foi adotado para homenagear Leonardo Pisano.
- Sequência de Fibonacci: A sequência que leva seu nome é um dos conceitos mais reconhecidos e estudados na matemática, com aplicações que vão além da teoria, influenciando ciência, arte e a natureza.
Fibonacci!
Leonardo Fibonacci foi um matemático pioneiro cujo trabalho teve um impacto profundo e duradouro na matemática e na ciência. Suas viagens e estudos permitiram que ele trouxesse para a Europa conhecimentos matemáticos avançados, como o sistema numérico hindu-arábico e métodos algébricos e geométricos, que foram fundamentais para o desenvolvimento da matemática moderna. A Sequência de Fibonacci, em particular, continua a fascinar e influenciar diversas áreas do conhecimento. Suas obras, incluindo “Liber Abaci”, “Practica Geometriae”, “Flos”, “Liber Quadratorum” e “Di minor guisa”, oferecem um testemunho duradouro de seu gênio e contribuição para o avanço da matemática.
Este artigo foi elaborado pelo site Deep Wiki, especializado em fornecer informações detalhadas e precisas sobre o mercado financeiro e outras áreas do conhecimento.
Referências:
- Andean Calculators
- Lista com os 2000 primeiros números da sequência de Fibonacci. <https://oeis.org/A000045/b000045.txt>. Consultado em 09 de maio de 2016
- «Sequência Fibonacci». 13 de fevereiro de 2022
- S. Douady and Y. Couder (1996). «Phyllotaxis as a Dynamical Self Organizing Process» (PDF). Journal of Theoretical Biology. 178 (178): 255–274. doi:10.1006/jtbi.1996.0026. Consultado em 20 de janeiro de 2011. Arquivado do original (PDF) em 26 de maio de 2006
- Jones, Judy; William Wilson (2006). «Science». An Incomplete Education. [S.l.]: Ballantine Books. p. 544.
- A. Brousseau (1969). «Fibonacci Statistics in Conifers». Fibonacci Quarterly (7): 525–532
- Susantha Goonatilake (1998). Toward a Global Science. [S.l.]: Indiana University Press. p. 126.
- Singh, Parmanand (1985). «The So-called Fibonacci numbers in ancient and medieval India». Historia Mathematica. 12 (3): 229–244. doi:10.1016/0315-0860(85)90021-7
- Donald Knuth (1968). The Art Of Computer Programming, Volume 1. [S.l.]: Addison Wesley.
- Mathematics – “How can I find an inverse to the Binet formula?”. <http://math.stackexchange.com/questions/374758/how-can-i-find-an-inverse-to-the-binet-formula>. Consultado em 09 de maio de 2016.
- Propriedades matemáticas dos números de Fibonacci. <http://pessoal.sercomtel.com.br/matematica/alegria/fibonacci/seqfib1.htm Arquivado em 4 de maio de 2016, no Wayback Machine.>. Consultado em 06 de maio de 2016.
- Wolfram MathWorld: Pascal’s Triangle. <http://mathworld.wolfram.com/PascalsTriangle.html>. Consultado em 06 de maio de 2016.
- Sumofcubes.pdf. <https://www.math.hmc.edu/~benjamin/papers/sumfibocubes.pdf>.
- Wolfram MathWorld <http://mathworld.wolfram.com/TribonacciNumber.html>.
- ↑ Vera W. de Spinadel (1999). The Family of Metallic Means, Vismath 1(3) from Mathematical Institute of Serbian Academy of Sciences and Arts.
- de Spinadel, Vera W. (1998). Williams, Kim, ed. «The Metallic Means and Design». Fucecchio (Florence): Edizioni dell’Erba. Nexus II: Architecture and Mathematics: 141–157
- Scott, T.C.; Marketos, P. (março de 2014), On the Origin of the Fibonacci Sequence (PDF), MacTutor History of Mathematics archive, University of St Andrews
- OEIS/A007629-Lista dos 94 primeiros números de Keith< http://oeis.org/A007629/b007629.txt >
















